Text: Wikipedia.
Enigma ist der Markenname und eine Sammelbezeichnung für eine Reihe von Rotor-Chiffriermaschinen, die seit den 1920er-Jahren zur Verschlüsselung von Nachrichten verwendet wurden. Im Zweiten Weltkrieg (1939-1945) wurden Enigma-Maschinen von den Achsenmächten eingesetzt, hauptsächlich von der Wehrmacht. Den Alliierten gelang es, die damit verschlüsselten Funksprüche nahezu kontinuierlich zu entziffern, was bis 1974 geheim gehalten wurde.
Dieser Artikel gibt eine Übersicht über die grundsätzliche Entwicklungsgeschichte der Enigma und ihre Funktionsweise. Dabei liegt der Schwerpunkt hier auf der im Jahr 1930 von der Reichswehr in Dienst gestellten Enigma I (sprich: „Enigma eins“), des während des Krieges am meisten verwendeten Modells. Zu den einzelnen Enigma-Modellen sowie zu speziellen Aspekten des Enigma-Chiffriersystems gibt es weiterführende Artikel mit teilweise deutlich ausführlicheren Erläuterungen.
Noch während der Zeit des Ersten Weltkriegs (1914-1918) suchten die deutschen Militärs nach einem Ersatz für die inzwischen veralteten, umständlichen und unsicheren manuellen Verschlüsselungsverfahren, wie Codebücher (siehe auch: Zimmermann-Depesche), ÜBCHI, ABC-Chiffre oder ADFGX, die bis dahin verwendet wurden. Hierfür kamen maschinelle Verfahren in Betracht, weil sie eine einfachere Handhabung und eine verbesserte kryptographische Sicherheit versprachen. Mit Einführung der elektrischen Schreibmaschine und des Fernschreibers zu Beginn des 20. Jahrhunderts kamen zum Teil unabhängig voneinander und nahezu gleichzeitig mehrere Erfinder auf die Idee des Rotor-Prinzips zur Verschlüsselung von Texten.
Erfinder der Enigma ist Arthur Scherbius (1878-1929), dessen erstes Patent hierzu vom 23. Februar 1918 stammt (siehe auch: Enigma-Patente). Im Frühjahr 1917 stand er in Diensten des Waffen- und Munitionsbeschaffungsamts (WuMBA) und war vom Kriegsministerium beauftragt worden, eine geeignete Schlüsselmaschine zu entwickeln. Ein Jahr später führte er eine erste von mindestens drei Probemaschinen vor, die zur Anzeige Glühlämpchen verwendeten. Im April 1918 war er dazu zunächst im Großen Hauptquartier in Spa und wenige Wochen später im Reichsmarineamt in Berlin. Die Kaiserliche Marine testete die Maschine und lobte deren „gute Schlüsselsicherheit“, kam aber zu dem Schluss, dass „vorläufig bei der Art des Marine-Schlüsselverkehrs die Anwendung von Maschinen nicht lohnen würde“.
Die „Handelsmaschine“ (1923) war nach den „Probemaschinen“ (1918) die erste in einer langen Reihe von Enigma-Modellen. Nach dem Krieg beschloss Scherbius, die Maschine für zivile Anwendungen zu vermarkten. Zur Fertigung wurde am 9. Juli 1923 die Chiffriermaschinen-Aktiengesellschaft (ChiMaAG) in Berlin gegründet. Das erste in etwas größeren Stückzahlen gefertigte Modell war 1923 eine „schreibende“ Enigma, genannt die „Handelsmaschine“. Sie nutze keine Glühlämpchen zur Textausgabe, sondern wie Schreibmaschinen ein Typenrad. Ihr folgte ein Jahr später die „Schreibende Enigma“, auch als „Typenhebelchiffriermaschine“ bezeichnet, die statt des Typenrads übliche Typenhebel verwendete. Die neuen Chiffriermaschinen wurden kommerziell auf Messen zum Kauf angeboten, erwiesen sich jedoch als wenig zuverlässig und wurden kein kommerzieller Erfolg.
Da die deutschen Militärs eine Wiederholung der inzwischen bekannt gewordenen kryptographischen Katastrophe des Ersten Weltkriegs unbedingt vermeiden wollten, betrachteten sie die neue Art der maschinellen Verschlüsselung als die sicherste Lösung. Im Jahr 1926 wurde ein anderes Enigma-Modell, nun wieder mit Glühlämpchen, zunächst von der Reichsmarine unter dem Namen „Funkschlüssel C“, zwei Jahre später auch vom Heer versuchsweise eingesetzt und verschwand daraufhin vom zivilen Markt. Es wurde fortan weiterentwickelt und ab 1927 zunächst in Stückzahlen von einigen Hundert im Geheimen gefertigt. Als „kryptographische Komplikation“ erhielt es zusätzlich ein geheimes „Schaltbrett“ an der Frontplatte, aus dem etwas später das Enigma-Steckerbrett wurde. Am 1. Juni 1930 wurde dieses Modell unter dem Namen „Enigma I“ von der Reichswehr offiziell in Dienst gestellt und in den folgenden Jahren in großer Serie gefertigt. Man schätzt, dass insgesamt etwa 40.000 Enigma-Maschinen hergestellt wurden.
Arthur Scherbius erlebte den kommerziellen Erfolg seiner Idee nicht mehr. Er war am 13. Mai 1929 den tödlichen Verletzungen erlegen, die er sich kurz zuvor bei einem Verkehrsunfall zugezogen hatte. Unter der am 31. Juli 1935 in Berlin neu gegründeten Firma „Chiffriermaschinen Gesellschaft Heimsoeth und Rinke oHG“, kurz „Heimsoeth & Rinke“ (H&R), wurde die Geschäftstätigkeit unter der Leitung von Rudolf Heimsoeth und Elsbeth Rinke fortgesetzt. Unter Federführung ihres Oberingenieurs Willi Korn, der seit 1926 bei der ChiMaAG war, wurde die Enigma-Produktfamilie verbessert und erweitert. Neben der Enigma I, die während des Zweiten Weltkriegs das auf deutscher Seite am häufigsten benutzte Maschinenschlüsselverfahren verkörperte, kamen im Laufe der Zeit auch andere Modelle und Varianten der Enigma zum Einsatz, beispielsweise die Enigma-G bei der deutschen Abwehr oder ab Oktober 1941 die Enigma-M4 im Nachrichtenverkehr der deutschen Kriegsmarine.
Nach Ende des Krieges wurden die beispielsweise in der Schweiz vorhandenen Maschinen eine Zeit lang dort weiterverwendet und von Schweizer Soldaten auch in Korea genutzt. In Norwegen von der Wehrmacht zurückgelassene Exemplare wurden dort modifiziert und als „Norenigma“ eingesetzt.
Die wichtigsten Funktionsgruppen der Enigma I.
Alle Enigma-Glühlampenchiffriermaschinen, wie insbesondere die Enigma I, bestehen im Wesentlichen aus der Tastatur zur Buchstabeneingabe, einem Walzensatz zur Verschlüsselung und einem Glühlampenfeld zur Anzeige. Bei der Enigma I sind es drei Walzen, die nebeneinander unabhängig drehbar angeordnet sind und ausgetauscht werden können. Zum Austausch standen zunächst nur drei und ab 1938 dann insgesamt fünf Walzen zur Verfügung.
Drückt man eine Buchstabentaste, so fließt elektrischer Strom durch den Walzensatz und lässt eine Anzeigelampe aufleuchten. Der aufleuchtende Buchstabe entspricht der Verschlüsselung des gedrückten Buchstabens. Da sich bei jedem Tastendruck die Walzen ähnlich wie bei einem mechanischen Kilometerzähler weiterdrehen, ändert sich das geheime Schlüsselalphabet nach jedem Buchstaben.
Aufbau
Die Enigma I inklusive Holzgehäuse wiegt rund 12 kg und die äußeren Abmessungen (L×B×H) betragen etwa 340 mm × 280 mm × 150 mm[11] (Daten ohne Gehäuse: 10,35 kg und 310 mm × 255 mm × 130 mm).
Ihr Erfinder sagte: „Die Maschine ist ganz ähnlich einer Schreibmaschine gebaut und wird auch genau wie diese bedient.“ Die Buchstabenlampen und Eingabetasten sind bei den meisten Enigma-Modellen (Ausnahmen sind die chronologisch vor der Enigma-D hergestellten) ähnlich der im deutschen Sprachraum heute gebräuchlichen QWERTZ-Belegung angeordnet. Jedoch sind die Buchstaben P und L abweichend davon an die äußeren Ränder der unteren Reihe verschoben:
Q W E R T Z U I O
A S D F G H J K
P Y X C V B N M L
Es gab auch Enigma-Modelle, die Ziffern aufwiesen, wie die Enigma-D oder die Enigma-Z, oder sogar Sonderzeichen, wie die Enigma-G. Die Enigma-B kannte auch Umlaute und in einer speziellen Variante den im Schwedischen verwendeten Buchstaben Å.
Die Maschine nutzt drei auswechselbare rotierende Walzen (Rotoren) mit jeweils 26 Stellungen. Bei Heer und Luftwaffe waren diese auf einem außen auf der Walze befindlichen drehbaren Ring mit den Zahlen 01 bis 26 bezeichnet. Bei der Kriegsmarine verwendete man stattdessen die Buchstaben A bis Z. Der Ring lässt sich unabhängig von der Walze in eine beliebige von 26 Positionen einstellen (Ringstellung). Rechts der drei drehbaren Walzen (Walzensatz) befindet sich eine unbewegliche Eintrittswalze (ETW). Links befindet sich die Umkehrwalze (UKW) als Reflektor, die, im Gegensatz zu vielen frühen Enigma-Maschinen, bei den meistverwendeten Modellen, insbesondere bei der Enigma I, weder drehbar noch für den Anwender austauschbar ist. Alle Walzen sind über 26 einzelne Schleifkontakte miteinander elektrisch verbunden.
Als zusätzliche „kryptographische Komplikation“ ist an der Gerätefront ein Steckerbrett mit doppelpoligen Steckbuchsen für jeden der 26 Buchstaben angebracht. Die Buchsenanordnung entspricht der Tastaturbelegung.
Funktion
Beim Drücken einer Buchstabentaste wird die rechte Walze um einen Schritt weitergedreht und ein Stromkreis geschlossen, der solange geschlossen bleibt, wie die Taste gedrückt ist. Bei beispielsweise der Buchstabentaste A wird der Batteriestrom über die Taste A zur gleichnamigen Buchse im Steckerbrett durchgeschaltet. Ist dort die Buchse A mit einer anderen Buchse durch ein von außen angebrachtes Kabel verbunden („gesteckert“), so wird A mit einem anderen Buchstaben vertauscht. Ist kein Kabel gesteckt („ungesteckert“), dann gelangt der Strom direkt zum Kontakt A der Eintrittswalze.
Angenommen der Buchstabe A sei ungesteckert, dann wird der Strom über die Eintrittswalze zum Eingangskontakt A der rechten Walze geleitet. Deren Verdrahtung bewirkt eine Substitution (Ersetzung) des Buchstabens durch einen anderen oder durch denselben. Der Strom, der am Eingangskontakt A von rechts eintritt, verlässt die Walze auf deren linken Seite am Ausgangskontakt B. So wird durch die rechte Walze der Buchstabe A durch B ersetzt.
Stromfluss
Der Strom gelangt nun über den Kontakt B in die mittlere Walze. Da es bei der Verdrahtung einer Walze durchaus möglich ist, dass ein Eingangskontakt mit dem gleichnamigen Ausgangskontakt verbunden ist, bleibt B hier unverändert. Der Strom verlässt über Kontakt B die mittlere Walze und tritt in die linke Walze ein. Deren Verdrahtung sorgt dafür, dass der Strom vom Eingangskontakt B zum Ausgangskontakt D geleitet wird. Der Strom hat nun alle drei (drehbaren) Walzen einmal durchlaufen und die Umkehrwalze erreicht. Sie hat nur Kontakte auf der rechten Seite und verbindet Buchstaben paarweise, beispielsweise D mit E.
Nun fließt der Strom ein zweites Mal durch den Walzensatz, jetzt aber von links nach rechts. Durch die Umkehrwalze gelangt er über den Kontakt E in die linke Walze. Hier ist beispielsweise E mit C verdrahtet. Folglich fließt der Strom weiter über Kontakt C in die mittlere Walze, verlässt sie wieder über den Kontakt F und fließt in die rechte Walze. Der Strom verlässt die rechte Walze schließlich am Kontakt G.
Nach Austritt aus dem Walzensatz wird der Strom über die Eintrittswalze zurück zum Steckerbrett geleitet. Ist hier der Buchstabe G mit einem anderen Buchstaben gesteckert, dann findet eine letzte Permutation statt. Ist G ungesteckert, leuchtet die Lampe G auf. Sie leuchtet nur solange auf, wie die Taste A gedrückt gehalten wird, da nur bei gedrückter Taste der Umschaltkontakt auf die Batterie umgeschaltet ist. Lässt man sie los, erlischt die Lampe. Im geschilderten Beispiel wird somit der Buchstabe A, dessen Taste eingangs gedrückt wurde und noch immer gedrückt ist, als Buchstabe G verschlüsselt.
Falls der zu verschlüsselnde Text „AACHENISTGERETTET“ lautet, ist erneut ein A einzugeben. Also wird die Taste A losgelassen und zum zweiten Mal gedrückt. Der mechanische Druck auf die Taste bewegt die rechte Walze erneut um eine Position weiter. Die mittlere Walze rotiert erst nach 26 Schritten der rechten Walze (Ausnahme: Anomalie), die linke Walze erst nach 26 Schritten der mittleren Walze.
Der Pfad für den erneut am Kontakt A der rechten Walze eintretenden Strom hat sich nun radikal geändert . Er nimmt jetzt auch bei der mittleren und linken Walze sowie der Umkehrwalze einen völlig anderen Weg als zuvor, auch wenn sich diese Walzen nicht gedreht haben, was ja nur relativ selten geschah. Das Ergebnis ist eine andere Verschlüsselung des Buchstabens A, der nun in C umgewandelt wird.
Enigma ist der Markenname und eine Sammelbezeichnung für eine Reihe von Rotor-Chiffriermaschinen, die seit den 1920er-Jahren zur Verschlüsselung von Nachrichten verwendet wurden. Im Zweiten Weltkrieg (1939-1945) wurden Enigma-Maschinen von den Achsenmächten eingesetzt, hauptsächlich von der Wehrmacht. Den Alliierten gelang es, die damit verschlüsselten Funksprüche nahezu kontinuierlich zu entziffern, was bis 1974 geheim gehalten wurde.
Dieser Artikel gibt eine Übersicht über die grundsätzliche Entwicklungsgeschichte der Enigma und ihre Funktionsweise. Dabei liegt der Schwerpunkt hier auf der im Jahr 1930 von der Reichswehr in Dienst gestellten Enigma I (sprich: „Enigma eins“), des während des Krieges am meisten verwendeten Modells. Zu den einzelnen Enigma-Modellen sowie zu speziellen Aspekten des Enigma-Chiffriersystems gibt es weiterführende Artikel mit teilweise deutlich ausführlicheren Erläuterungen.
Noch während der Zeit des Ersten Weltkriegs (1914-1918) suchten die deutschen Militärs nach einem Ersatz für die inzwischen veralteten, umständlichen und unsicheren manuellen Verschlüsselungsverfahren, wie Codebücher (siehe auch: Zimmermann-Depesche), ÜBCHI, ABC-Chiffre oder ADFGX, die bis dahin verwendet wurden. Hierfür kamen maschinelle Verfahren in Betracht, weil sie eine einfachere Handhabung und eine verbesserte kryptographische Sicherheit versprachen. Mit Einführung der elektrischen Schreibmaschine und des Fernschreibers zu Beginn des 20. Jahrhunderts kamen zum Teil unabhängig voneinander und nahezu gleichzeitig mehrere Erfinder auf die Idee des Rotor-Prinzips zur Verschlüsselung von Texten.
Erfinder der Enigma ist Arthur Scherbius (1878-1929), dessen erstes Patent hierzu vom 23. Februar 1918 stammt (siehe auch: Enigma-Patente). Im Frühjahr 1917 stand er in Diensten des Waffen- und Munitionsbeschaffungsamts (WuMBA) und war vom Kriegsministerium beauftragt worden, eine geeignete Schlüsselmaschine zu entwickeln. Ein Jahr später führte er eine erste von mindestens drei Probemaschinen vor, die zur Anzeige Glühlämpchen verwendeten. Im April 1918 war er dazu zunächst im Großen Hauptquartier in Spa und wenige Wochen später im Reichsmarineamt in Berlin. Die Kaiserliche Marine testete die Maschine und lobte deren „gute Schlüsselsicherheit“, kam aber zu dem Schluss, dass „vorläufig bei der Art des Marine-Schlüsselverkehrs die Anwendung von Maschinen nicht lohnen würde“.
Die „Handelsmaschine“ (1923) war nach den „Probemaschinen“ (1918) die erste in einer langen Reihe von Enigma-Modellen. Nach dem Krieg beschloss Scherbius, die Maschine für zivile Anwendungen zu vermarkten. Zur Fertigung wurde am 9. Juli 1923 die Chiffriermaschinen-Aktiengesellschaft (ChiMaAG) in Berlin gegründet. Das erste in etwas größeren Stückzahlen gefertigte Modell war 1923 eine „schreibende“ Enigma, genannt die „Handelsmaschine“. Sie nutze keine Glühlämpchen zur Textausgabe, sondern wie Schreibmaschinen ein Typenrad. Ihr folgte ein Jahr später die „Schreibende Enigma“, auch als „Typenhebelchiffriermaschine“ bezeichnet, die statt des Typenrads übliche Typenhebel verwendete. Die neuen Chiffriermaschinen wurden kommerziell auf Messen zum Kauf angeboten, erwiesen sich jedoch als wenig zuverlässig und wurden kein kommerzieller Erfolg.
Da die deutschen Militärs eine Wiederholung der inzwischen bekannt gewordenen kryptographischen Katastrophe des Ersten Weltkriegs unbedingt vermeiden wollten, betrachteten sie die neue Art der maschinellen Verschlüsselung als die sicherste Lösung. Im Jahr 1926 wurde ein anderes Enigma-Modell, nun wieder mit Glühlämpchen, zunächst von der Reichsmarine unter dem Namen „Funkschlüssel C“, zwei Jahre später auch vom Heer versuchsweise eingesetzt und verschwand daraufhin vom zivilen Markt. Es wurde fortan weiterentwickelt und ab 1927 zunächst in Stückzahlen von einigen Hundert im Geheimen gefertigt. Als „kryptographische Komplikation“ erhielt es zusätzlich ein geheimes „Schaltbrett“ an der Frontplatte, aus dem etwas später das Enigma-Steckerbrett wurde. Am 1. Juni 1930 wurde dieses Modell unter dem Namen „Enigma I“ von der Reichswehr offiziell in Dienst gestellt und in den folgenden Jahren in großer Serie gefertigt. Man schätzt, dass insgesamt etwa 40.000 Enigma-Maschinen hergestellt wurden.
Arthur Scherbius erlebte den kommerziellen Erfolg seiner Idee nicht mehr. Er war am 13. Mai 1929 den tödlichen Verletzungen erlegen, die er sich kurz zuvor bei einem Verkehrsunfall zugezogen hatte. Unter der am 31. Juli 1935 in Berlin neu gegründeten Firma „Chiffriermaschinen Gesellschaft Heimsoeth und Rinke oHG“, kurz „Heimsoeth & Rinke“ (H&R), wurde die Geschäftstätigkeit unter der Leitung von Rudolf Heimsoeth und Elsbeth Rinke fortgesetzt. Unter Federführung ihres Oberingenieurs Willi Korn, der seit 1926 bei der ChiMaAG war, wurde die Enigma-Produktfamilie verbessert und erweitert. Neben der Enigma I, die während des Zweiten Weltkriegs das auf deutscher Seite am häufigsten benutzte Maschinenschlüsselverfahren verkörperte, kamen im Laufe der Zeit auch andere Modelle und Varianten der Enigma zum Einsatz, beispielsweise die Enigma-G bei der deutschen Abwehr oder ab Oktober 1941 die Enigma-M4 im Nachrichtenverkehr der deutschen Kriegsmarine.
Nach Ende des Krieges wurden die beispielsweise in der Schweiz vorhandenen Maschinen eine Zeit lang dort weiterverwendet und von Schweizer Soldaten auch in Korea genutzt. In Norwegen von der Wehrmacht zurückgelassene Exemplare wurden dort modifiziert und als „Norenigma“ eingesetzt.
Die wichtigsten Funktionsgruppen der Enigma I.
Alle Enigma-Glühlampenchiffriermaschinen, wie insbesondere die Enigma I, bestehen im Wesentlichen aus der Tastatur zur Buchstabeneingabe, einem Walzensatz zur Verschlüsselung und einem Glühlampenfeld zur Anzeige. Bei der Enigma I sind es drei Walzen, die nebeneinander unabhängig drehbar angeordnet sind und ausgetauscht werden können. Zum Austausch standen zunächst nur drei und ab 1938 dann insgesamt fünf Walzen zur Verfügung.
Drückt man eine Buchstabentaste, so fließt elektrischer Strom durch den Walzensatz und lässt eine Anzeigelampe aufleuchten. Der aufleuchtende Buchstabe entspricht der Verschlüsselung des gedrückten Buchstabens. Da sich bei jedem Tastendruck die Walzen ähnlich wie bei einem mechanischen Kilometerzähler weiterdrehen, ändert sich das geheime Schlüsselalphabet nach jedem Buchstaben.
Aufbau
Die Enigma I inklusive Holzgehäuse wiegt rund 12 kg und die äußeren Abmessungen (L×B×H) betragen etwa 340 mm × 280 mm × 150 mm[11] (Daten ohne Gehäuse: 10,35 kg und 310 mm × 255 mm × 130 mm).
Ihr Erfinder sagte: „Die Maschine ist ganz ähnlich einer Schreibmaschine gebaut und wird auch genau wie diese bedient.“ Die Buchstabenlampen und Eingabetasten sind bei den meisten Enigma-Modellen (Ausnahmen sind die chronologisch vor der Enigma-D hergestellten) ähnlich der im deutschen Sprachraum heute gebräuchlichen QWERTZ-Belegung angeordnet. Jedoch sind die Buchstaben P und L abweichend davon an die äußeren Ränder der unteren Reihe verschoben:
Q W E R T Z U I O
A S D F G H J K
P Y X C V B N M L
Es gab auch Enigma-Modelle, die Ziffern aufwiesen, wie die Enigma-D oder die Enigma-Z, oder sogar Sonderzeichen, wie die Enigma-G. Die Enigma-B kannte auch Umlaute und in einer speziellen Variante den im Schwedischen verwendeten Buchstaben Å.
Die Maschine nutzt drei auswechselbare rotierende Walzen (Rotoren) mit jeweils 26 Stellungen. Bei Heer und Luftwaffe waren diese auf einem außen auf der Walze befindlichen drehbaren Ring mit den Zahlen 01 bis 26 bezeichnet. Bei der Kriegsmarine verwendete man stattdessen die Buchstaben A bis Z. Der Ring lässt sich unabhängig von der Walze in eine beliebige von 26 Positionen einstellen (Ringstellung). Rechts der drei drehbaren Walzen (Walzensatz) befindet sich eine unbewegliche Eintrittswalze (ETW). Links befindet sich die Umkehrwalze (UKW) als Reflektor, die, im Gegensatz zu vielen frühen Enigma-Maschinen, bei den meistverwendeten Modellen, insbesondere bei der Enigma I, weder drehbar noch für den Anwender austauschbar ist. Alle Walzen sind über 26 einzelne Schleifkontakte miteinander elektrisch verbunden.
Als zusätzliche „kryptographische Komplikation“ ist an der Gerätefront ein Steckerbrett mit doppelpoligen Steckbuchsen für jeden der 26 Buchstaben angebracht. Die Buchsenanordnung entspricht der Tastaturbelegung.
Funktion
Beim Drücken einer Buchstabentaste wird die rechte Walze um einen Schritt weitergedreht und ein Stromkreis geschlossen, der solange geschlossen bleibt, wie die Taste gedrückt ist. Bei beispielsweise der Buchstabentaste A wird der Batteriestrom über die Taste A zur gleichnamigen Buchse im Steckerbrett durchgeschaltet. Ist dort die Buchse A mit einer anderen Buchse durch ein von außen angebrachtes Kabel verbunden („gesteckert“), so wird A mit einem anderen Buchstaben vertauscht. Ist kein Kabel gesteckt („ungesteckert“), dann gelangt der Strom direkt zum Kontakt A der Eintrittswalze.
Angenommen der Buchstabe A sei ungesteckert, dann wird der Strom über die Eintrittswalze zum Eingangskontakt A der rechten Walze geleitet. Deren Verdrahtung bewirkt eine Substitution (Ersetzung) des Buchstabens durch einen anderen oder durch denselben. Der Strom, der am Eingangskontakt A von rechts eintritt, verlässt die Walze auf deren linken Seite am Ausgangskontakt B. So wird durch die rechte Walze der Buchstabe A durch B ersetzt.
Stromfluss
Der Strom gelangt nun über den Kontakt B in die mittlere Walze. Da es bei der Verdrahtung einer Walze durchaus möglich ist, dass ein Eingangskontakt mit dem gleichnamigen Ausgangskontakt verbunden ist, bleibt B hier unverändert. Der Strom verlässt über Kontakt B die mittlere Walze und tritt in die linke Walze ein. Deren Verdrahtung sorgt dafür, dass der Strom vom Eingangskontakt B zum Ausgangskontakt D geleitet wird. Der Strom hat nun alle drei (drehbaren) Walzen einmal durchlaufen und die Umkehrwalze erreicht. Sie hat nur Kontakte auf der rechten Seite und verbindet Buchstaben paarweise, beispielsweise D mit E.
Nun fließt der Strom ein zweites Mal durch den Walzensatz, jetzt aber von links nach rechts. Durch die Umkehrwalze gelangt er über den Kontakt E in die linke Walze. Hier ist beispielsweise E mit C verdrahtet. Folglich fließt der Strom weiter über Kontakt C in die mittlere Walze, verlässt sie wieder über den Kontakt F und fließt in die rechte Walze. Der Strom verlässt die rechte Walze schließlich am Kontakt G.
Nach Austritt aus dem Walzensatz wird der Strom über die Eintrittswalze zurück zum Steckerbrett geleitet. Ist hier der Buchstabe G mit einem anderen Buchstaben gesteckert, dann findet eine letzte Permutation statt. Ist G ungesteckert, leuchtet die Lampe G auf. Sie leuchtet nur solange auf, wie die Taste A gedrückt gehalten wird, da nur bei gedrückter Taste der Umschaltkontakt auf die Batterie umgeschaltet ist. Lässt man sie los, erlischt die Lampe. Im geschilderten Beispiel wird somit der Buchstabe A, dessen Taste eingangs gedrückt wurde und noch immer gedrückt ist, als Buchstabe G verschlüsselt.
Falls der zu verschlüsselnde Text „AACHENISTGERETTET“ lautet, ist erneut ein A einzugeben. Also wird die Taste A losgelassen und zum zweiten Mal gedrückt. Der mechanische Druck auf die Taste bewegt die rechte Walze erneut um eine Position weiter. Die mittlere Walze rotiert erst nach 26 Schritten der rechten Walze (Ausnahme: Anomalie), die linke Walze erst nach 26 Schritten der mittleren Walze.
Der Pfad für den erneut am Kontakt A der rechten Walze eintretenden Strom hat sich nun radikal geändert . Er nimmt jetzt auch bei der mittleren und linken Walze sowie der Umkehrwalze einen völlig anderen Weg als zuvor, auch wenn sich diese Walzen nicht gedreht haben, was ja nur relativ selten geschah. Das Ergebnis ist eine andere Verschlüsselung des Buchstabens A, der nun in C umgewandelt wird.
ENIGMA WIRKUNG.
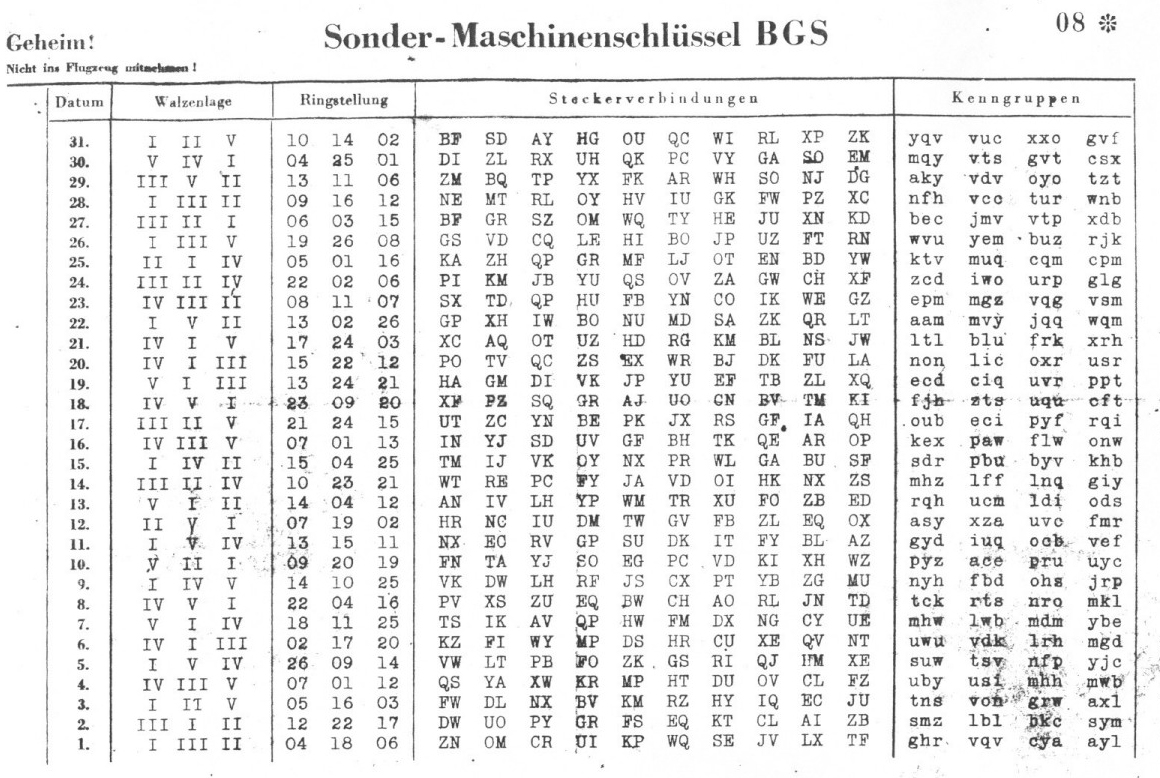
Diese Schlüsseltafel des Heeres listet die täglich wechselnden Teilschlüssel „Walzenlage“, „Ringstellung“ und „Steckerverbindungen“ für einen Monat auf.
Bei der Enigma I standen zunächst drei, ab 1939 dann fünf unterschiedliche Walzen zur Verfügung, die mit römischen Zahlen <https://de.wikipedia.org/wiki/R%C3%B6mische_Zahlschrift> (I, II, III, IV und V) durchnummeriert waren. Der Benutzer wählte nach Vorgabe einer geheimen Schlüsseltabelle, die für jeden Tag wechselnde Einstellungen vorsah, drei Walzen aus und setzte diese nach der im Tagesschlüssel <https://de.wikipedia.org/wiki/Tagesschl%C3%BCssel> unter der Überschrift „Walzenlage“ vorgeschriebenen Anordnung ein.
Die „Schlüsseltafel <https://de.wikipedia.org/wiki/Schl%C3%BCsseltafel>“ stellte tabellarisch für einen kompletten Monat die jeweils gültigen Tagesschlüssel dar, die beim Heer um Mitternacht gewechselt wurden und bei der Luftwaffe um 3 Uhr nachts. Unten sind beispielhaft nur drei Monatstage dargestellt, wobei, wie damals üblich, die Tage absteigend sortiert sind. Dies erlaubt es dem Verschlüssler, die verbrauchten Codes der vergangenen Tage abzuschneiden und zu vernichten.
Beispiel für den 29. des Monats: Walzenlage „I IV III“ bedeutet, dass hier Walze I links (als langsamer Rotor), Walze IV in der Mitte und Walze III rechts (als schneller Rotor) eingesetzt werden musste. Als Umkehrwalze wurde - wie bereits erwähnt - zumeist ausschließlich die UKW B benutzt.
Die Ringe, die außen an jedem Walzenkörper angebracht sind und den Rotationsversatz zwischen der inneren Verdrahtung der Walzen und den außen zu sehenden Buchstaben oder Zahlen bestimmen, sind jeweils auf die für den Tag vorgegebenen Stellungen zu drehen, genannt die „Ringstellung“. Dazu muss von Hand ein durch eine Blattfeder eingedrückter Haltestift ausgezogen werden, der nach Einstellen und Loslassen die eingestellte Stellung arretiert. Im Beispiel hier 16 26 08 entsprechend P Z H.
Tag Walzenlage Ringstellung ---- Steckerverbindungen ----
31 III I IV 01 17 22 AH BL CX DI ER FK GU NP OQ TY
30 II V I 18 24 11 BN DZ EP FX GT HW IY OU QV RS
29 I IV III 16 26 08 AD CN ET FL GI JV KZ PU QY WX
Example
Bei der Enigma I standen zunächst drei, ab 1939 dann fünf unterschiedliche Walzen zur Verfügung, die mit römischen Zahlen <https://de.wikipedia.org/wiki/R%C3%B6mische_Zahlschrift> (I, II, III, IV und V) durchnummeriert waren. Der Benutzer wählte nach Vorgabe einer geheimen Schlüsseltabelle, die für jeden Tag wechselnde Einstellungen vorsah, drei Walzen aus und setzte diese nach der im Tagesschlüssel <https://de.wikipedia.org/wiki/Tagesschl%C3%BCssel> unter der Überschrift „Walzenlage“ vorgeschriebenen Anordnung ein.
Die „Schlüsseltafel <https://de.wikipedia.org/wiki/Schl%C3%BCsseltafel>“ stellte tabellarisch für einen kompletten Monat die jeweils gültigen Tagesschlüssel dar, die beim Heer um Mitternacht gewechselt wurden und bei der Luftwaffe um 3 Uhr nachts. Unten sind beispielhaft nur drei Monatstage dargestellt, wobei, wie damals üblich, die Tage absteigend sortiert sind. Dies erlaubt es dem Verschlüssler, die verbrauchten Codes der vergangenen Tage abzuschneiden und zu vernichten.
Beispiel für den 29. des Monats: Walzenlage „I IV III“ bedeutet, dass hier Walze I links (als langsamer Rotor), Walze IV in der Mitte und Walze III rechts (als schneller Rotor) eingesetzt werden musste. Als Umkehrwalze wurde - wie bereits erwähnt - zumeist ausschließlich die UKW B benutzt.
Die Ringe, die außen an jedem Walzenkörper angebracht sind und den Rotationsversatz zwischen der inneren Verdrahtung der Walzen und den außen zu sehenden Buchstaben oder Zahlen bestimmen, sind jeweils auf die für den Tag vorgegebenen Stellungen zu drehen, genannt die „Ringstellung“. Dazu muss von Hand ein durch eine Blattfeder eingedrückter Haltestift ausgezogen werden, der nach Einstellen und Loslassen die eingestellte Stellung arretiert. Im Beispiel hier 16 26 08 entsprechend P Z H.
Tag Walzenlage Ringstellung ---- Steckerverbindungen ----
31 III I IV 01 17 22 AH BL CX DI ER FK GU NP OQ TY
30 II V I 18 24 11 BN DZ EP FX GT HW IY OU QV RS
29 I IV III 16 26 08 AD CN ET FL GI JV KZ PU QY WX
Example
Source: NARA, Washington DC, US.
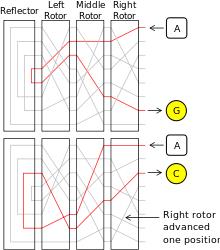
Bij het voor de tweede keer indrukken van de letter A op het toetsenbord, draait de rechter rotor 1 positie door, de middelste en de linker rotor blijven stilstaan. De refector draait überhaupt niet.
De middelste rotor draait pas 1 postie, wanneer de rechter rotor alle 26 posities heeft gehad.
De middelste rotor draait pas 1 postie, wanneer de rechter rotor alle 26 posities heeft gehad.
Der Text (plus der späteren Kenngruppe) weist hier eine Länge von 167 Buchstaben auf. Der Verschlüssler hat seine Enigma, wie oben beschrieben, entsprechend dem Tagesschlüssel, beispielsweise für den 29. des Monats, eingestellt, also Walzenlage B I IV III, Ringstellung 16 26 08 und Steckerverbindungen AD CN ET FL GI JV KZ PU QY WX. Sowohl dieser als auch die im Folgenden beschriebenen Schritte können mithilfe von Enigma Stimulationen realitätsnah nachvollzogen werden.
Der Bediener denkt sich nun eine zufällige Grundstellung aus, beispielsweise „QWE“ (17 23 05), und stellt die drei Walzen so ein, dass genau diese drei Buchstaben in den Anzeigefenstern sichtbar werden. Nun lässt er sich einen zufälligen Spruchschlüssel ebenfalls mit drei Buchstaben einfallen, beispielsweise „RTZ“. Diesen verschlüsselt er mit seiner Enigma und beobachtet, wie nacheinander die Lampen „EWG“ aufleuchten. Den so verschlüsselten Spruchschlüssel teilt er dem Empfänger zusammen mit der zufällig gewählten Grundstellung als Indikator sowie der Uhrzeit und der Anzahl der Buchstabenzahl als „Spruchkopf“ offen mit.
De bediener van de Enigma machine bedenkt zelf een 'Basisinstelling', bijvoorbeeld QWE (dit komt overeen met de getallen 17, 23 & 05 op de rotors) en zo stelt hij de drie rotors in. Vervolgens bedenk hij de berichtcode ook bestaande uit drie letters, RTZ. Deze drie letters versleutelt hij met de Enigma machine en de uitkomst is nu dat RTZ gecodeerd EWG wordt. Hij stuurt de willekeurig gekozen Basisinstelling ook wel Ídikator' genoemd samen met de tijd en het aantal letters van het bericht naar de ontvanger. Dit alles noemt men de 'Spruchkopf' of Header.
De vraag is: waarom doet hij dit? Er is immers voor elke dag een blad die alle instellingen aangeeft.
Laut damals geltender Dienstvorschriften der Wehrmacht Nr. 14 enthält der Spruchkopf die Uhrzeit, beispielsweise 22:20 Uhr als vierstellige Zahl, also „2220“, die Buchstabenanzahl des Spruchs, hier „167“, die gewählte Grundstellung, hier „QWE“, und den verschlüsselten Spruchschlüssel, hier „EWG“. Der Spruchkopf würde hier also lauten:
2220 167 = qwe ewg =
De tijd is dus 22:20 uur, het aantal letters is 167, de ringinstelling is QWE en de berichtcode is EWG..
De 'Spruchschlüssel'(berichtcode) is de rotor instelling voor het bericht zelf. De Kopregel wordt met een andere rotor instelling verzonden.
Als Nächstes wählt der Bediener noch drei für diesen Tag gültige Kenngruppenbuchstaben anhand einer Kenngruppentabelle aus, beispielsweise „NOW“. Die Kenngruppe hat keine kryptologische Bedeutung,sie dient dem Empfänger der Nachricht nur dazu, zu erkennen, dass die Nachricht wirklich für ihn bestimmt ist und auch befugt entschlüsselt werden kann. Zur Verschleierung der Kenngruppe werden die drei Buchstaben vom Absender beliebig permutiert (verandering van volgorde) und um zwei für jeden Spruch zufällig zu wechselnde „Füllbuchstaben“,beispielsweise „XY“, ergänzt. Aus „NOW“ wird so zunächst etwa „OWN“ und schließlich „XYOWN“. Diese fünf Buchstaben werden unverschlüsselt als erste Fünfergruppe dem Geheimtext vorangestellt.
De Kenngruppencode bestaat uit drie letters die de ontvanger laten weten dat het bericht voor hem bestemd is. Bij SOE werd dit de Prefix genoemd. Bij SOE had de ontvanger een vaste prefix bestaande uit drie cijfers, Deze werd eventueel door SOE na enige verandert en dit kreeg de ontvanger via een radiobericht te horen.
De Duitse zender bepaalde dus uit een lijst de Kenngruppe (prefix) voor de ontvanger. Om de zoveel berichten werden de drie letters door elkaar gegooid. Ook werden letters toegevoegd. Elk bericht begon met de ongecodeerde Kenngruppe
Hoe wist de ontvanger dat het bericht voor hem bestemd was, de zendende partij had immers de Kenngruppe gekozen.
Der Verschlüssler stellt nun die drei Walzen seiner Enigma auf den von ihm gewählten Spruchschlüssel „RTZ“ (18 20 26) ein und verschlüsselt den obigen Klartext, das heißt, er gibt jeden einzelnen Buchstaben des Klartextes über die Tastatur der Enigma ein, liest die jeweils aufleuchtende Lampe als Geheimtextbuchstaben ab und notiert ihn. Zusammen mit dem Spruchkopf (obere Zeile) und der getarnten Kenngruppe (erste Fünfergruppe) ergibt sich der folgende Funkspruch:
2220 167 = qwe ewg = (tijd, aantal letters, ringinstelling van de rotors en de berichtsleutel)
XYOWN (Kenngruppe code, of prefix ongecodeerd) CCXQU BHTEG PLIIC FBVIJ ECLHZ KVCDQ IIILT LCJYR CXPSG IHRLD YTBIQ DOTUJ GQQWZ YJDQO FPKBU RNBPC NZRLP TUBXL XPZYJ XITNH KEWZE HEJKZ PVQDU ICRBA USDLG CDIVP HUGNL OQKFF KNWXF VIOMT SKBCC VQWAW SL
Dauer: 1 Minute und 38 Sekunden.1:38
Klangbeispiel einer Morseübertragung
Kopf und Geheimtext werden als Morsezeichen gefunkt und vom Empfänger aufgenommen. Dieser prüft als erstes, ob die Anzahl der Buchstaben (hier: 167) korrekt ist und der Spruch unverstummelt empfangen wurde. Dann betrachtet er die Kenngruppe, also die erste Fünfergruppe, ignoriert die ersten beiden Buchstaben und sieht „OWN“. Er sortiert die drei Buchstaben in alphabetischer Reihenfolge, erhält so „NOW“, schaut in seine Kenngruppentabelle, entdeckt dort diese Kenngruppenbuchstaben und kann nun sicher sein, dass der Spruch für ihn bestimmt ist und er ihn entschlüsseln kann. Seine Enigma ist bereits bezüglich Walzenlage, Ringstellung und Steckerverbindungen entsprechend dem auch ihm bekannten Tagesschlüssel identisch mit der des Absenders eingestellt. Es fehlt ihm noch der Spruchschlüssel, also die richtige Anfangsstellung der Walzen zur Entschlüsselung des Spruchs. Diese Information erhält er aus dem Indikator „= qwe ewg =“ im Spruchkopf, den er wie folgt interpretiert: Stelle die Walzen auf die Grundstellung „QWE“ (17 23 05) ein und taste dann „EWG“. Nun kann er beobachten, wie nacheinander die Lampen „RTZ“ bei seiner Enigma aufleuchten. Dies ist der einzustellende Spruchschlüssel.
Er dreht nun die Walzen auf die Anfangsstellung „RTZ“ (18 20 26) und beginnt, den Geheimtext, hier angefangen mit „CCXQU“, in seine Enigma einzugeben. Nun leuchten nacheinander die Lampen auf, der Klartext erscheint Buchstabe für Buchstabe, und er kann den folgenden Text notieren:
xaachenxaachenxistgerettetxdurqgebuendelteneinsatzderhilfskraeftekonntediebedrohungabgewendetunddierettungderstadtgegenx einsxaqtxnullxnullxuhrsiqergestelltwerdenx
Im Allgemeinen wurden handschriftlich alle Buchstaben kleingeschrieben, da sie so schneller notiert werden konnten als bei Gebrauch von Grossuchstaben.
Der Bediener denkt sich nun eine zufällige Grundstellung aus, beispielsweise „QWE“ (17 23 05), und stellt die drei Walzen so ein, dass genau diese drei Buchstaben in den Anzeigefenstern sichtbar werden. Nun lässt er sich einen zufälligen Spruchschlüssel ebenfalls mit drei Buchstaben einfallen, beispielsweise „RTZ“. Diesen verschlüsselt er mit seiner Enigma und beobachtet, wie nacheinander die Lampen „EWG“ aufleuchten. Den so verschlüsselten Spruchschlüssel teilt er dem Empfänger zusammen mit der zufällig gewählten Grundstellung als Indikator sowie der Uhrzeit und der Anzahl der Buchstabenzahl als „Spruchkopf“ offen mit.
De bediener van de Enigma machine bedenkt zelf een 'Basisinstelling', bijvoorbeeld QWE (dit komt overeen met de getallen 17, 23 & 05 op de rotors) en zo stelt hij de drie rotors in. Vervolgens bedenk hij de berichtcode ook bestaande uit drie letters, RTZ. Deze drie letters versleutelt hij met de Enigma machine en de uitkomst is nu dat RTZ gecodeerd EWG wordt. Hij stuurt de willekeurig gekozen Basisinstelling ook wel Ídikator' genoemd samen met de tijd en het aantal letters van het bericht naar de ontvanger. Dit alles noemt men de 'Spruchkopf' of Header.
De vraag is: waarom doet hij dit? Er is immers voor elke dag een blad die alle instellingen aangeeft.
Laut damals geltender Dienstvorschriften der Wehrmacht Nr. 14 enthält der Spruchkopf die Uhrzeit, beispielsweise 22:20 Uhr als vierstellige Zahl, also „2220“, die Buchstabenanzahl des Spruchs, hier „167“, die gewählte Grundstellung, hier „QWE“, und den verschlüsselten Spruchschlüssel, hier „EWG“. Der Spruchkopf würde hier also lauten:
2220 167 = qwe ewg =
De tijd is dus 22:20 uur, het aantal letters is 167, de ringinstelling is QWE en de berichtcode is EWG..
De 'Spruchschlüssel'(berichtcode) is de rotor instelling voor het bericht zelf. De Kopregel wordt met een andere rotor instelling verzonden.
Als Nächstes wählt der Bediener noch drei für diesen Tag gültige Kenngruppenbuchstaben anhand einer Kenngruppentabelle aus, beispielsweise „NOW“. Die Kenngruppe hat keine kryptologische Bedeutung,sie dient dem Empfänger der Nachricht nur dazu, zu erkennen, dass die Nachricht wirklich für ihn bestimmt ist und auch befugt entschlüsselt werden kann. Zur Verschleierung der Kenngruppe werden die drei Buchstaben vom Absender beliebig permutiert (verandering van volgorde) und um zwei für jeden Spruch zufällig zu wechselnde „Füllbuchstaben“,beispielsweise „XY“, ergänzt. Aus „NOW“ wird so zunächst etwa „OWN“ und schließlich „XYOWN“. Diese fünf Buchstaben werden unverschlüsselt als erste Fünfergruppe dem Geheimtext vorangestellt.
De Kenngruppencode bestaat uit drie letters die de ontvanger laten weten dat het bericht voor hem bestemd is. Bij SOE werd dit de Prefix genoemd. Bij SOE had de ontvanger een vaste prefix bestaande uit drie cijfers, Deze werd eventueel door SOE na enige verandert en dit kreeg de ontvanger via een radiobericht te horen.
De Duitse zender bepaalde dus uit een lijst de Kenngruppe (prefix) voor de ontvanger. Om de zoveel berichten werden de drie letters door elkaar gegooid. Ook werden letters toegevoegd. Elk bericht begon met de ongecodeerde Kenngruppe
Hoe wist de ontvanger dat het bericht voor hem bestemd was, de zendende partij had immers de Kenngruppe gekozen.
Der Verschlüssler stellt nun die drei Walzen seiner Enigma auf den von ihm gewählten Spruchschlüssel „RTZ“ (18 20 26) ein und verschlüsselt den obigen Klartext, das heißt, er gibt jeden einzelnen Buchstaben des Klartextes über die Tastatur der Enigma ein, liest die jeweils aufleuchtende Lampe als Geheimtextbuchstaben ab und notiert ihn. Zusammen mit dem Spruchkopf (obere Zeile) und der getarnten Kenngruppe (erste Fünfergruppe) ergibt sich der folgende Funkspruch:
2220 167 = qwe ewg = (tijd, aantal letters, ringinstelling van de rotors en de berichtsleutel)
XYOWN (Kenngruppe code, of prefix ongecodeerd) CCXQU BHTEG PLIIC FBVIJ ECLHZ KVCDQ IIILT LCJYR CXPSG IHRLD YTBIQ DOTUJ GQQWZ YJDQO FPKBU RNBPC NZRLP TUBXL XPZYJ XITNH KEWZE HEJKZ PVQDU ICRBA USDLG CDIVP HUGNL OQKFF KNWXF VIOMT SKBCC VQWAW SL
Dauer: 1 Minute und 38 Sekunden.1:38
Klangbeispiel einer Morseübertragung
Kopf und Geheimtext werden als Morsezeichen gefunkt und vom Empfänger aufgenommen. Dieser prüft als erstes, ob die Anzahl der Buchstaben (hier: 167) korrekt ist und der Spruch unverstummelt empfangen wurde. Dann betrachtet er die Kenngruppe, also die erste Fünfergruppe, ignoriert die ersten beiden Buchstaben und sieht „OWN“. Er sortiert die drei Buchstaben in alphabetischer Reihenfolge, erhält so „NOW“, schaut in seine Kenngruppentabelle, entdeckt dort diese Kenngruppenbuchstaben und kann nun sicher sein, dass der Spruch für ihn bestimmt ist und er ihn entschlüsseln kann. Seine Enigma ist bereits bezüglich Walzenlage, Ringstellung und Steckerverbindungen entsprechend dem auch ihm bekannten Tagesschlüssel identisch mit der des Absenders eingestellt. Es fehlt ihm noch der Spruchschlüssel, also die richtige Anfangsstellung der Walzen zur Entschlüsselung des Spruchs. Diese Information erhält er aus dem Indikator „= qwe ewg =“ im Spruchkopf, den er wie folgt interpretiert: Stelle die Walzen auf die Grundstellung „QWE“ (17 23 05) ein und taste dann „EWG“. Nun kann er beobachten, wie nacheinander die Lampen „RTZ“ bei seiner Enigma aufleuchten. Dies ist der einzustellende Spruchschlüssel.
Er dreht nun die Walzen auf die Anfangsstellung „RTZ“ (18 20 26) und beginnt, den Geheimtext, hier angefangen mit „CCXQU“, in seine Enigma einzugeben. Nun leuchten nacheinander die Lampen auf, der Klartext erscheint Buchstabe für Buchstabe, und er kann den folgenden Text notieren:
xaachenxaachenxistgerettetxdurqgebuendelteneinsatzderhilfskraeftekonntediebedrohungabgewendetunddierettungderstadtgegenx einsxaqtxnullxnullxuhrsiqergestelltwerdenx
Im Allgemeinen wurden handschriftlich alle Buchstaben kleingeschrieben, da sie so schneller notiert werden konnten als bei Gebrauch von Grossuchstaben.

Der Ring der mittleren Walze ist hier auf 01 eingestellt (siehe rotes Dreieck in der Mitte des Bildes). Dazu wurde der
Haltestift nach rechts seitlich herausgezogen und der nun frei auf dem Walzenkörper bewegliche Ring passend gedreht,
bis das rote Dreieck auf die hier vorgeschriebene „Ringstellung 01“ zeigte. Bei Loslassen rastet der Stift die Bohrung die
bei 01 ein (eine „leere“ ist darüber rechts neben 02 gut zu sehen). Dadurch wird der Ring arretiert und die vorgeschrie
bene Ringstellung ist eingestellt.
Die Größe des Schlüsselraums der Enigma lässt sich aus den vier einzelnen Teilschlüsseln sowie der Anzahl der jeweils
möglichen unterschiedlichen Schlüsseleinstellungen berechnen. Der gesamte Schlüsselraum der Enigma I ergibt sich aus den
folgenden vier Faktoren:
a) Die Walzenlage.
Drei von fünf Walzen (I bis V) werden ausgewählt. (Als Umkehrwalze wurde fast immer nur die UKW B benutzt.) Dies
ergibt 5x4x3=60 mögliche Walzenlagen (entspricht einer 'Schlüssellänge' von etwa 6 bit).
Six-bit character code is a character encoding designed for use on computers with word lengths a multiple of 6. Six bits can only encode
64 distinct characters, so these codes generally include only the upper-case letters, the numerals, some punctuation characters, and
sometimes control characters..
b) Die Ringstellung.
Es gibt jeweils 26 verschiedene Ringstelungen (01-26) für jede Walze (Rotor). Der Ring der linken Walze trägt nicht zur
Vergrösserung des Schlüsselraums bei, da seine mit dem Ring verbundene Übertragskerbe kein Fortschalten einer noch
weiter links befindliche Walze bewirkt. Ingesamt sind 2622 = 676 Ringstellungen relevant (entspricht etwa 9 bit).
c) Die Walzenstellung.
Es gibt für jede der drei (rotierenden) Walzen 26 Möglichkeiten, sie einzustellen (A bis Z). Die Umkehrwalze kann nicht
verstellt werden. Insgesamt sind somit 26³ = 17.576 Walzenstellungen verfügbar. Setzt man die Ringstellung als
bekannt voraus, so sind davon aufgrund einer unwichtigen Anomallie des Fortschaltmechnismus 26²-26 = 650
Anfangsstellungen als kryptographisch redundant zu eliminieren. Als relevant übrig bleiben dann 16.926
Walzenstellungen (entspricht etwa 14 bit).
d) Die Steckerverbindungen.
Es können bis zu 13 Steckerverbindungen zwischen den 26 Buchstaben hergestellt werden. Ausgehend vom Fall des
ungesteckerten Steckerbretts (in der Tabelle unten als Nummer 0 berücksichtigt), gibt es für die erste
Steckerverbindung 26 Auswahlmöglichkeiten für das eine Ende und dann noch 25 für das andere Ende des Kabels. Somit
gibt es für das erste Kabel 26·25 unterschiedliche Möglichkeiten, es einzustecken. Da es aber keine Rolle spielt, in
welcher Reihenfolge die beiden Kabelenden gesteckt werden, entfallen davon die Hälfte der Möglichkeiten. Es bleiben
also 26·25/2 = 325 Möglichkeiten für die erste Verbindung. Für die zweite erhält man analog 24·23/2 = 276
Möglichkeiten. Allgemein gibt es (26-2n+2)·(26-2n+1)/2 Möglichkeiten für die n-te Steckerverbindung.
Die Gesamtzahl der möglichen Steckkombinationen bei Verwendung von mehreren Steckern ergibt sich aus dem Product
der Möglichkeiten für die einzelnen Steckerverbindungen. Da aber auch hier die Reihenfolge der Durchführung keine Rolle
spielt (es ist kryptographisch gleichwertig, wenn beispielsweise zuerst A mit X gesteckert wird und danach B mit Y oder
umgekehrt zuerst B mit Y und dann A mit X), dürfen die entsprechenden Fälle nicht als Schlüsselkombinationen
berücksichtigt werden. Dies sind bei zwei Steckerverbindungen genau die Hälfte der Fälle. Das vorher ermittelte Produkt
ist also durch 2 zu dividieren. Bei drei Steckerverbindungen gibt es sechs mögliche Reihenfolgen für die Durchführung
der Steckungen, die alle sechs kryptographisch gleichwertig sind. Das Produkt ist also durch 6 zu dividieren. Im
allgemeinen Fall, bei n Steckerverbindungen, ist das Produkt der vorher ermittelten Möglichkeiten durch n! (Fakultät) zu
dividieren. Die Anzahl der Möglichkeiten für genau n Steckerverbindungen
Nachdem in den ersten Jahren nur sechs und später zwischen fünf und acht Verbindungskabel gesteckt wurden, galt ab
August 1939 die feste Regel, stets genau zehn Steckerverbindungen durchzuführen. Für diese ergeben sich nach der
obigen Tabelle 150.738.274.937.250 (mehr als 150 Billionen) Steckmöglichkeiten (entspricht etwa 47 bit).
Der gesamte Schlüsselraum einer Enigma I mit drei aus einem Vorrat von fünf ausgewählten Walzen und einer
Umkehrwalze sowie bei Verwendung von zehn Steckern lässt sich aus dem Produkt der in den obigen Abschnitten a) bis
d) ermittelten 60 Walzenlagen, 676 Ringstellungen, 16.926 Walzenstellungen und 150.738.274.937.250 Stecker
möglichkeiten berechnen. Er beträgt:
60 · 676 · 16.926 · 150.738.274.937.250 = 103.484.623.446.804.960.360.000
Das sind etwa 10²³ Möglichkeiten und entspricht einer Schlüssellänge von ungefähr 76 bit. Die gelegentlich zu hörenden
„150 Millionen Millionen Millionen“ Kombinationen, Die genaue Rechnung ergibt in diesem Fall 60 · 16.926 ·
150.738.274.937.250 oder 153.083.762.495.273.610.000 unterschiedliche Fälle, wobei die Briten zumeist statt 16.926
alle 26³ oder 17.576 mögliche Walzenstellungen berücksichtigten und als Produkt dann 158.962.555.217.826.360.000
erhielten.
Der Schlüsselraum war für die damalige Zeit enorm groß und hält sogar einem Vergleich mit moderneren Verfahren
stand. Beispielsweise verfügt das über mehrere Jahrzehnte gegen Ende des 20. Jahrhunderts zum Standard erhobene
Verschlüsselungsverfahren DES (Data Encryption Standard) über eine Schlüssellänge von genau 56 bit, also deutlich
weniger als die Enigma. Eine Exhaustion (vollständiges Durchsuchen) des Schlüsselraums der Enigma ist selbst mit
modernen Mitteln kaum möglich und war mit der damaligen Technologie vollkommen illusorisch.
Zwar ist eine ausreichend große Schlüssellänge eine notwendige Bedingung für die Sicherheit (praktische
„Unbrechbarkeit“) eines kryptographischen Verfahrens, aber eine große Schlüssellänge allein bietet keinerlei Garantie
dafür. So verfügt die deutlich simplere Methode der einfachen monoalphabetischen Substitution (bei Verwendung eines
Alphabets aus 26 Buchstaben wie die Enigma) über 26! (Fakultät) mögliche Schlüssel; das sind grob 4000 x 1023
Schlüssel (ungefähr 88 bit) und verglichen mit der Zahl 10²³ der Enigma I sogar noch 4000 mal mehr. Dennoch ist eine
monoalphabetische Substitution sehr unsicher und kann leicht gebrochen (entziffert) werden.
Auch bei der Enigma ähnelt die wesentlich zur Größe des Schlüsselraums beitragende konstruktive Komponente, nämlich
das Steckerbrett, einer einfachen monoalphabetischen Substitution, denn die Steckerung bleibt schließlich während der
gesamten Verschlüsselung unverändert. Das Steckerbrett kann folglich mithilfe einer intelligenten kryptanalytischen
Angriffsmethode (Turing Bombe) überwunden und praktisch gänzlich eliminiert werden. Damit kann der Faktor
150.738.274.937.250 bei der Berechnung des Schlüsselraums effektiv wieder gestrichen werden.
Ebenso bewirken die Ringe nur eine geringe kryptographische Stärkung des Verfahrens. Bei falscher Ringstellung der rechten Walze und ansonsten
korrektem Schlüssel sind periodisch (Periodenlänge = 26 Buchstaben) bereits Klartextpassagen lesbar, die jeweils nach
einigen Buchstaben immer wieder abreißen. Noch weniger wirkt der Ring der mittleren Walze, wobei hier die
Periodenlänge 650 Buchstaben (25 x 26) beträgt. Die mittlere Ringstellung trägt somit zumeist überhaupt nicht zur
Größe des Schlüsselraums bei, immer dann nämlich, wenn während des Spruchs kein Übertrag auf die linke Walze
erfolgt, der aufgrund der vorgeschriebenen Spruchlänge von höchstens 250 Buchstaben nur selten passierte. Die
Ringstellung der linken Walze ist aus kryptanalytischer Sicht völlig bedeutungslos. Insgesamt stellt die Feinjustierung
der Ringe keine größere Schwierigkeit für den Kryptoanalytiker dar. Damit kann man bei der Berechnung der Größe des
Schlüsselraums auch den Faktor 676 getrost wieder streichen.
Als kryptographisch wirksam übrig bleiben nur die 60 Walzenlagen und die (bei unbekannter Ringstellung) 17.576 zu
berücksichtigenden Walzenstellungen. So schrumpft der vorher noch so gigantisch erscheinende Schlüsselraum auf
vergleichsweise winzige 60·17.576 = 1.054.560 (gut eine Million) Möglichkeiten (etwa 20 bit), eine Zahl, die auch
bereits zu Zeiten des Zweiten Weltkriegs mithilfe der damaligen elektromechanischen Technik exhaustiv (erschöpfend)
abgearbeitet werden konnte.
w.mugge@home.nl
Walzensatz aus drei rotierenden Walzen und der Umkehrwalze B (links):
